Hall–Janko graph
| Hall–Janko graph | |
|---|---|
HJ as Foster graph (90 outer vertices) plus Steiner system S(3,4,10) (10 inner vertices). |
|
| Named after | Zvonimir Janko Marshall Hall |
| Vertices | 100 |
| Edges | 1800 |
| Radius | 2 |
| Diameter | 2 |
| Girth | 3 |
| Chromatic number | 10 |
| Properties | Strongly regular Vertex-transitive Cayley graph Eulerian Hamiltonian Integral |
In the mathematical field of graph theory, the Hall–Janko graph, also known as the Hall-Janko-Wales graph, is a 36-regular undirected graph with 100 vertices and 1800 edges.[1]
It is a rank 3 strongly regular graph with parameters (100,36,14,12) and a maximum coclique of size 10. This parameter set is not unique, it is however uniquely determined by its parameters as a rank 3 graph. The Hall–Janko graph was originally constructed by D. Wales to establish the existence of the Hall-Janko group as an index 2 subgroup of its automorphism group.
The Hall–Janko graph can be constructed out of objects in U3(3), the simple group of order 6048[2][3]:
- In U3(3) there are 36 simple maximal subgroups of order 168. These are the vertices of a subgraph, the U3(3) graph. A 168-subgroup has 14 maximal subgroups of order 24, isomorphic to S4. Two 168-subgroups are called adjacent when they intersect in a 24-subgroup. The U3(3) graph is strongly regular, with parameters (36,14,4,6)
- There are 63 involutions (elements of order 2). A 168-subgroup contains 21 involutions, which are defined to be neighbors.
- Outside U3(3) let there be a 100th vertex C, whose neighbors are the 36 168-subgroups. A 168-subgroup then has 14 common neighbors with C and in all 1+14+21 neighbors.
- An involution is found in 12 of the 168-subgroups. C and an involution are non-adjacent, with 12 common neighbors.
- Two involutions are defined as adjacent when they generate a dihedral subgroup of order 8.[4] An involution has 24 involutions as neighbors.
The characteristic polynomial of the Hall–Janko graph is 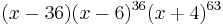 . Therefore the Hall–Janko graph is an integral graph: its spectrum consists entirely of integers.
. Therefore the Hall–Janko graph is an integral graph: its spectrum consists entirely of integers.
References
- ^ Weisstein, Eric W., "Hall-Janko graph" from MathWorld.
- ^ Andries E. Brouwer, "Hall-Janko graph".
- ^ Andries E. Brouwer, "U3(3) graph".
- ^ Robert A. Wilson, 'The Finite Simple Groups', Springer-Verlag (2009), p. 224.